Statistical Investigation of Aloha Packet Radio Transmission
By Steve Edwards 30/4/2010
1) Distinguish between Pure and Slotted Aloha (10)
1) Identify the Probability Distribution used to analyse the performance of the systems and manner in which it is applied to the situations (10)
2) Identify the maximum throughput of both Pure and Slotted ALOHA (5)
3) Apply the appropriate probability distribution to both Pure and Slotted ALOHA and develop expressions for:
a) Probability of zero collisions (20)
b) Throughput (10)
4) Referring to differential calculus explain how the maximum throughput can be determined (20)
Introduction
In the 1970s, a system of packet radio communications was developed by Norman Abramson to link computer terminals on the five main islands of Hawaii, via a base station who’s reception could be “captured” or not, for the duration of the sending stations frame time. Successful capture and therefore successful transmission and processing of the sent frame by the base station depended on many factors beyond the scope of this document, including:
receiver capture
performance
distance from the
central receiver, path loss
channel fading and
dispersion
shadowing
contending frame traffic
(from same cell)
interference from
co-channel cells
channel noise
modulation method
bit rate
type of coding, frame
length
signal processing at
the receiver (diversity, equalization, ...)
access protocol:
slotted ALOHA, Carrier Sense (CSMA) or Inhibit Sense Multiple Access (ISMA).
http://www.wirelesscommunication.nl/reference/chaptr06/capture.htm
[online] date accessed 6/4/10
Q1) Distinguish between Pure and
Slotted Aloha
Investigation of only the effects that “contending frame traffic” has (i.e. collisions of frames from other stations transmitting at the same time) found that Pure ALOHA was inherently unstable for multiple users under certain conditions, as the base station sent an acknowledgment to the sending station ONLY on successful receipt of data, but if the sending station did not receive an acknowledgment, it assumed the frame to be lost, and retransmitted the frame after a random time period. This could give rise to further collisions and so further re-transmissions, effectively clogging the system to a point where no successful transmissions/receipts could occur.
This transmission method is known as “blind transmission” as the sending station has no knowledge of the state of other system users when it transmits data, as there is no innate mechanism for the radio medium to feedback collision information to the system users, as exists for copper electronic based media via the detection of an overvoltage due to the collisions on the wire, by the network card.
http://www.wirelesscommunication.nl/reference/chaptr06/capture.htm
[online] date accessed 6/4/10
An improvement to Pure Aloha was the development of Slotted Aloha, whereby the reception period of the base station is divided into defined “time slots” with a specific beginning time (T0) for the acceptance of a sent frame. Each user station is then “synchronised” by timing data sent from the base station, interleaved between its frame receipt slots, so is aware of the available time slot when it can transmit data it has to send.
This cuts down on the probability of overall collisions from other stations’ purely randomly timed frames of Pure Aloha, that can collide from before and during a current transmission attempt, (i.e. over a period of TWO frame times for Pure Aloha) to only stations that are ready to send in the same slot time.
A random “back off” algorithm is still implemented before a station can retransmit, as in Pure Aloha.
This time slot method increases the overall throughput of data for a given system, compared to Pure Aloha, as we shall see.
Various other methods were devised to further improve the efficiency of collision based systems, such as the Dynamic Frame Length algorithm.
http://www.wirelesscommunication.nl/reference/audio/intervws/schoute2.mp3
[online] date accessed 6/4/10
Q2) Identify the Probability
Distribution used to analyse the performance of the systems and manner in which
it is applied to the situations
From the explanation above, it is noted that the time periods being examined for the analysis of the probability of success for the transmission of a particular frame for Pure and Slotted Aloha systems are 2 frame slots and 1 frame slot respectively. This time period, T is known as the vulnerable period, where 2 frames can collide, and is 1T long for Slotted and 2T long for Pure Aloha.
The use of Poisson for Aloha systems analysis assumes: a population of up to infinite users; a fixed transmission speed; a frame is error free; frame transmission is successful if there are no collisions; all frames are the same length over any time period T; assumes a Poisson probability distribution for both Aloha systems.
Another assumption made by using the Poisson analysis are that the probability of a given number of conflicting frames being transmitted during the same frame time is small compared to the probability of no frames being transmitted at all i.e. there is always a good chance of a successful transmission of a frame in any frame time.
http://www.wirelesscommunication.nl/reference/appendix/poisson.htm
[online] date accessed 6/4/10
The Poison distribution probability analysis is applied to this communication system to find the probability of successful frame transmissions out of the total transmission attempts per frame time using the equation:
Pn =
(Np)^n x e^(-Np)
n!
Where:
Pn = Probability of the number of transmission attempts, n, per time period T
p = probability of successful frames sent per time period T
N=Number of system users that can transmit at any time (stations)
Np = M = mean number of transmission attempts per time period T
n! = factorial n
e = Eulers Number = 2.71828…
0! =1
To calculate the probability of a sent frame being successful for Pure Aloha over a time period 2T, we need Pn where n=0, i.e. where no other frames are sent by another user so no collisions occur within the time period 2T. As the time period is twice as long as Slotted Aloha, the probability for the number of transmissions in this time is doubled to 2Np.
P(n) = (2Np)^n x e^(-2Np)
n!
When n=0, this becomes:
P(0) = 1 x e^(-2Np)
0!
= e^(-2Np)
For Slotted Aloha, over a single time period T, the probability of successful transmission when n=0 becomes
P(0) = (Np)^0 x e^(-Np)
0!
= e^-Np
Q3) Identify the maximum throughput
of both Pure and Slotted ALOHA
The throughput, S, of a system can be defined as useful data sent by the system in a given time period, or the number of attempts (Np) at sending a frame multiplied by the probability of successful transmission of that frame [e^(-2Np)] in a given time period.
The probability of success for a frame is given above for each system, so this is multiplied by the mean number of user attempts, Np.
Substituting G for Np from the above equations:
S = Np x e^-2Np = Ge^-2G for Pure Aloha
And:
S = Np x e^-Np = Ge^-G for Slotted Aloha
For both systems the mean number of attempts, G, for a successful transmission needs to be 1 only in any frame time slot, for zero collisions, so the throughput, S is simply:
S = e^-2G = 1/ (2 x 2.71828) = 0.1839 or 18.4% for Pure Aloha
S = e^-G = 1/e for Slotted = 0.3678 or 36.8% for Slotted Aloha
The data throughput is approximately twice as much for Slotted as for Pure Aloha.
http://www.cs.sunysb.edu/~jgao/CSE370-spring07/aloha-analysis.pdf
[online] date accessed 6/4/10
Q4) Apply the appropriate probability
distribution to both Pure and Slotted ALOHA and develop expressions for:
a)
Probability
of zero collisions
The probability of zero collisions is what we wish to determine so a system can be optimised for successfully transmitting a frame.
From above we have the general Poisson probability equation:
Pn = (Np)^n
x e^(-Np)
n!
where Pn is the probability of occurrence of a particular number of events, n in a given time (1 single time period in this case for Slotted Aloha).
Np is the mean number of those occurrences in a given time period, and e = Eulers Number = 2.71828.
The probability of zero collisions is when no other user (stations) frames transmit in the same frame time as any other, so occurs when n=0:
P0 = (Np)^0 x e^(-Np) = 1. e^(-Np) = e^(-1) = 0.368 for Slotted Aloha
0! 1
P0 = (2Np)^0 x e^(-Np) = 1. e^(-2Np) = e^(-1) = 0.184 for Pure Aloha
0! 1
b)
Throughput
The throughput, S, of a system can be defined as useful data sent by the system in a given time period, or the number of attempts (Np) at sending a frame multiplied by the probability of successful transmission of that frame [e^(-2Np)] in a given time period.
Q5) Referring to differential
calculus explain how the maximum throughput can be determined
If data for a range 0-2 in 0.1 increments is graphed in
terms of both of the above equations, two curves, each with different maxima
are generated as shown below from an Excel spreadsheet. These curves represent
the data throughput S plotted against G, where S is the mean of new frames generated per frame time and G is the
mean of transmission attempts.
As each curve has a
maximum value, we can infer that differential calculus can also be used, using
the Product Rule for differentiation to obtain the first differential, to
determine the values for maximum throughput, S, as it is the value when the
slopes of the curves = 0 (the maximum in these cases). The differential
calculations can then be verified against the graph. From above, S = e^-2G
= 1/ (2 x 2.71828) = 0 for a differential maxima.
Pure Aloha Slotted Aloha
|
G |
G x e^(-2G) |
G |
G x e^(-G) |
|
|
0 |
0 |
0 |
0 |
|
|
0.1 |
0.081872484 |
0.1 |
0.0904834 |
|
|
0.2 |
0.134062073 |
0.2 |
0.163745 |
|
|
0.3 |
0.164639923 |
0.3 |
0.2222431 |
|
|
0.4 |
0.179726393 |
0.4 |
0.2681241 |
|
|
0.5 |
0.183933078 |
0.5 |
0.3032599 |
|
|
0.6 |
0.180708696 |
0.6 |
0.3292798 |
|
|
0.7 |
0.172609147 |
0.7 |
0.3476009 |
|
|
0.8 |
0.161507882 |
0.8 |
0.3594528 |
|
|
0.9 |
0.148759329 |
0.9 |
0.3659008 |
|
|
1 |
0.135325508 |
1 |
0.3678662 |
|
|
1.1 |
0.121873791 |
1.1 |
0.3661436 |
|
|
1.2 |
0.108852109 |
1.2 |
0.3614174 |
|
|
1.3 |
0.096546586 |
1.3 |
0.3542747 |
|
|
1.4 |
0.085125479 |
1.4 |
0.3452183 |
|
|
1.5 |
0.074672512 |
1.5 |
0.3346771 |
|
|
1.6 |
0.06521199 |
1.6 |
0.3230158 |
|
|
1.7 |
0.056727593 |
1.7 |
0.3105429 |
|
|
1.8 |
0.049176306 |
1.8 |
0.2975187 |
|
|
1.9 |
0.042498634 |
1.9 |
0.2841609 |
|
|
2 |
0.036625986 |
2 |
0.270651 |
Graph of Throughput (S) / G for Pure and Slotted Aloha
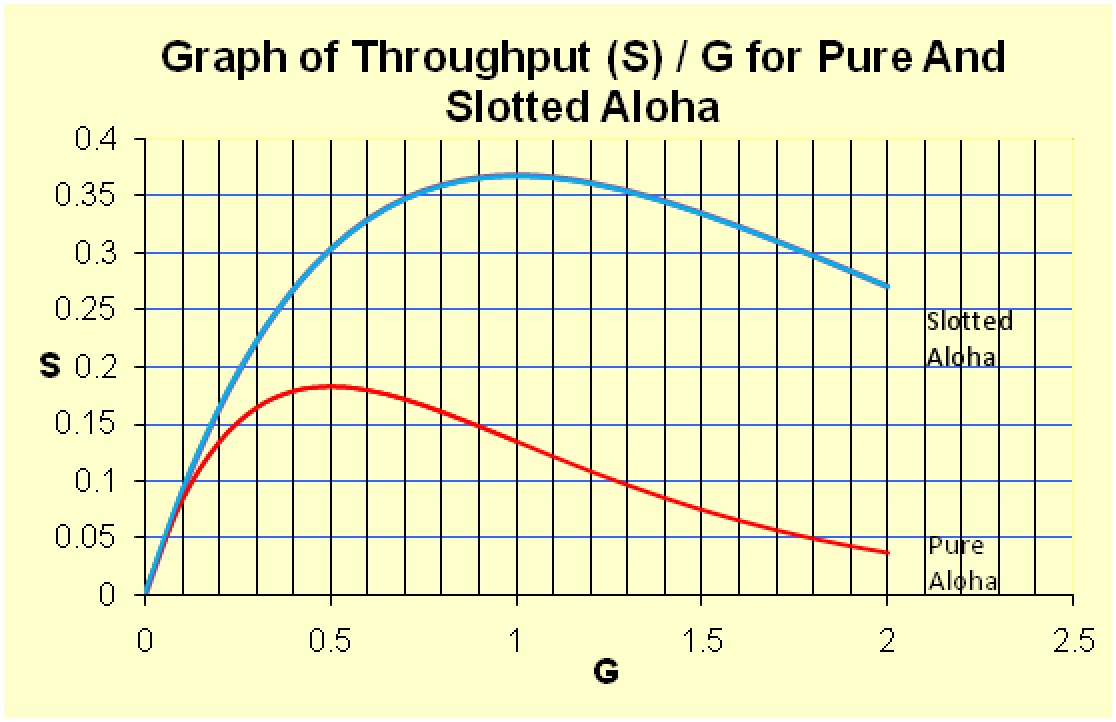
Equations:
S=Ge^(-2G) = 1/2e
where S is the mean of new frames generated per frame time and G is the mean of
transmission attempts, e = 2.71828
0.184 is the maximum
throughput when G = 0.5 as shown on the graph for Pure Aloha and below by
calculation as dS/dG = 0 at this point.
S=Ge^(-2G) = 1/2e
Let U = e^(-2G), so
S = GU,
so dU/dG =
-2e^(-2G) and
dG/dG = 1
Using Product Rule;
y=UV
dy/dx = U.dV/dx X V.dU/dx
Substituting for S
for y, and G for V in the Product Rule:
S = UG where
U=[e^(-2G)] we can differentiate with respect to G
dS/dG =
U.dG/dG + G.dU/dG
The first
differential of e^ax is ae^ax where a
is a constant, so the -2 = a in our case:
dS/dG =
[e^(-2G)].dG/dG + G.d[e^(-2G)]/dG
dS/dG = e^(-2G) . 1
+ G . [-2e^(-2G)]
The first
differential, dS/dG gives the slope of the curve = 0
dS/dG = 0 =
-2Ge^(-2G) + e^(-2G)
Adding +2Ge^(-2G)
to both sides:
2G/e^2G = 1/e^2G
And multiplying both
sides by e^2G to separate G:
G = ½
Substituting this
value back into the original S = Ge^(-2G) we do indeed get S =
0.5e(-1) = 0.184 or 18.4% of the available
bandwidth (bits/second)
Repeating for Slotted Aloha:
S = e^-G
dS/dG = [e^(-G)].dG/dG + G.d[e^(-G)]/dG
dS/dG = e^(-G) . 1
+ G . [-e^(-G)
The first
differential, dS/dG gives the slope of the curve = 0
dS/dG = 0 =
-Ge^(-G) + e^(-G)
Adding +Ge^(-G) to
both sides:
G/e^G = 1/e^G
And multiplying
both sides by e^G to separate G:
G = 1
Substituting this
value back into the original S = Ge^(-G) we do indeed get S =
1e(-1) = 0.368
or 36.8% of the available bandwidth (bits/second)
http://www.examsolutions.co.uk/maths-tutorials/differentiation/Product-Rule/Product-Rule-1.php
[online] date
accessed 7/4/10
References
http://www.wirelesscommunication.nl/reference/chaptr06/capture.htm
http://www.wirelesscommunication.nl/reference/chaptr06/aloha/darknite.htm
http://www.wirelesscommunication.nl/reference/chaptr06/aloha/aloha.htm
http://www.wirelesscommunication.nl/reference/audio/intervws/schoute2.mp3
http://www.wirelesscommunication.nl/reference/chaptr06/capture.htm
http://www.universalteacherpublications.com/univ/free-asgn/mcs42/page2.htm
http://www.comnets.uni-bremen.de/typo3site/uploads/media/0_exercise12.pdf
http://www.examsolutions.co.uk/maths-tutorials/differentiation/Product-Rule/Product-Rule-1.php